Random Generation Framework

So I set out last night to continue working on the "feature painting" design, then got really sidetracked into the wonderful world of random number generation.

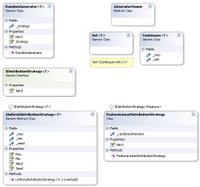
This is the class diagram I was messing around with. The original idea was to use this as an opportunity to experiment with generics, so I started with an abstract, generic RandomGenerator<T> class that would, conceptually, serve as a top-level class for producing random things. To create random numbers, I'd implement a RandomGenerator<int> or RandomGenerator<float>. But I also wanted to create random tiles or features as well. In fact, I'll eventually want to be able to randomize virtually any property of the game.

I just had an idea. Just now.

Anyway, I said to myself, "OK, this is good kind of class to have. Making it generic will serve to benefit me later if I build other generics that accept RandomGenerators." But then I started to realize that numbers, tiles, features, etc. don't all fit into the same classification of selectable things...

While I was thinking about implementing RandomGenerators for int and float types, it occured to me that I will probably want the ability to define, at runtime, a strategy by which the RandomGenerator chooses what numbers to output. That got me investigating probability distributions, and I learned plenty of fascinating things about discrete and continuous distributions and how greek they are. But the fact remained that, at least when choosing numbers, I'd like to be able to affect the selection by somehow instructing the RandomGenerator to use a uniform, logarithmic, Poisson — whatever — distribution.

But how to you apply such distributions to collections of tiles or features? Does it make semantic sense to say, "choose from among these objects using a uniform distribution?" Yes, in that case every object in the set has an identical probability of being selected. But I can't make semantic sense out of "choose from among these objects using a logarithmic distribution." To me, with my earthworm-like understanding of probability, such an action requires a sorted list. But how do you sort a list of tiles?

It occured to me that when selecting from a list of objects like tiles or features, the list in question will likely be a collection of object/probability pairs, not just object references. Each entry in the collection (Dictionary<Type, float>?) would identify a thing (unique to the set) and a probability that that thing will be chosen if something is selecting things from the set. This seems like a good idea, but I still can't wrap the idea of a logarithmic distribution around it. In this case, it seems like accomplishing a logarithmic distribution would be a matter of defining the pairs' probabilities according to a logarithmic curve. That makes defining the probabilities my responsibility, and as I'm sure you all know I don't like to work when I can get a computer to do it for me.

So I'm stuck on this: how do I come up with the RandomGenerator<T> class I seek? How do I make it so simple that all the user (me now or plugin developers later) has to do is implement (or if I make the class concrete, instantiate) RandomGenerator<WHATEVER> and get something useful out of that?

The diagram above is a fractured representation of my thoughts last night. I was trying to create an abstraction above the idea of a set and a continuum, and have that abstraction (a "source") serve as the pool from which a RandomGenerator selects its output. But ultimately I ran into this wall: a generator of random numbers is fundamentally a different engine that a random selector of things from a set. But I'm not sure they should be. I'm trying to get over this wall at the moment.

Faced with this problem, I decided to take a step back and regroup my thoughts. I could spend the next several months coming up with a really cool random generation framework, but I'm still itching to have a tech demo of a map generator. These are the thoughts I had. Clearly I couldn't completely tear myself away from the problem.

I'm obsessive like that.